×à ñò II. ÍÅËÈÍÅÉÍÀ ÐÅÃÐÅÑÈß*
2.1 ÂúâåäåГГЁГҐГЌГ ГЁГўГГ® ГҐ äà ñå ñìÿòà , Г·ГҐ Г¬Гîãîîáðà çГГЁГІГҐ âðúçêè ìåæäó çà îáèêà ëÿùèòå ГГЁ ÿâëåГГЁГї ìîãà ò äà áúäà ò îáÿñГГҐГГЁ åäèГГ±ГІГўГҐГГ® Г± ïîìîùòà Гà åäèГ-åäèГГ±ГІГўГҐГ ГіГèâåðñà ëåà ìîäåë. ГЊГ ГЄГ Г° ëèГГҐГ©Гà òà ðåãðåñèÿ äà ñå èçïîëçâà óñïåøГГ® çà èçñëåäâà ГГҐ Г±ГєГ± çà äîâîëèòåëГà çà ïðà êòèêà òà òî÷Гîñò ГГ ГҐГ¤Гà ãîëÿìà ÷à ñò îò ГЁГòåðåñóâà ùèòå ГГЁ âðúçêè ГЁ çà âèñèìîñòè, ГІГї ГГҐ ГҐ Гў ñúñòîÿГГЁГҐ äà îáÿñГГЁ à äåêâà òГГ® ðåäèöà âçà èìîäåéñòâèÿ ïîä÷èГГїГўГ Г№ГЁ Г±ГҐ ГГ ГҐГ¤ГГЁ ГЇГ®-ñëîæГГЁ ÊÐÈÂÎËÈÍÅÉÍÈ çà êîГîìåðГîñòè. ГЂГЄГ® ëèГГҐГ©ГГЁГїГІ ìîäåë Г±ГҐ îêà æå Гåà äåêâà òåà Гà äåéñòâèòåëГîñòòà , ГГҐ ГГЁ îñòà âà ГГЁГ№Г® äðóãî îñâåà äà ãî èçîñòà âèì ГЁ ïîòúðñèì äðóã ГЇГ®-ïîäõîäÿù ìîäåë, ГҐГ±ГІГҐГ±ГІГўГҐГГ® îòГîâî Г± ïîìîùòà Гà … ìà òåìà òèêà òà .
* ÂñúùГîñò òîâà Гà èìåГîâà ГГЁГҐ ГГҐ ГҐ Г±ГєГўГ±ГҐГ¬ òî÷ГГ®, ГГ® ïîðà äè øèðîêîòî ðà çïðîñòðà ГГҐГГЁГҐ, âêëþ÷èòåëГГ® ГЁ Гў ñåðèîçГГЁ èçòî÷Гèöè Г№ГҐ èçïîëçâà ìå ГГҐГЈГ®. Г‚ äåéñòâèòåëГîñò, ГҐГ¤Гà ëèГГЁГї (Гў îáùèÿ ñëó÷à é) ìîæå äà áúäå ïðà âà èëè êðèâà , çà òîâà ïðà âèëГГЁГїГІ òåðìèà ñïîðåä ìåà å „êðèâîëèГГҐГ©Гà ðåãðåñèÿ”.2.2 Ìà òåìà òè÷åñêè ìîäåëÑ èçó÷à âà ГГҐГІГ® ГГ ГґГіГêöèîГГ Г«ГГЁГІГҐ çà âèñèìîñòè Г±ГҐ çà Гèìà âà ñïåöèà ëåà êëîà Гà ìà òåìà òèêà òà – ìà òåìà òè÷åñêèÿ Г Гà ëèç. ГЌГЁГҐ Гÿìà äà çà äúëáà âà ìå Г·Г ГЄ òîëêîâà è Г№ГҐ Г±ГҐ îãðà ГГЁГ·ГЁГ¬ äî ðà çãëåæäà ГГҐГІГ® ГГ Гÿêîé
åëåìåГГІГ Г°ГГЁ ìà òåìà òè÷åñêè ГґГіГêöèè (ïîâå÷åòî èçó÷à âà ГГЁ Гў ñðåäГîòî ó÷èëèùå), êîèòî ñà ïîëó÷èëè øèðîêî ïðèëîæåГГЁГҐ çà ðåøà âà ГГҐГІГ® Гà ðà çëè÷ГГЁ çà äà ÷è Гў ïðà êòèêà òà . Г’Г ГЄГЁГўГ ГґГіГêöèè Г±Г Г±ГІГҐГЇГҐГГГ , ïîêà çà òåëГГ , ГҐГЄГ±ГЇГ®ГГҐГöèà ëГГ , ëîãà ðèòìè÷ГГ , ïà ðà áîëè÷ГГ , õèïåðáîëè÷ГГ ГЁ äðóãè, ГЄГ ГЄГІГ® ГЁ Гÿêîè êîìáèГà öèè ìåæäó ГІГїГµ.
Г…ГІГ® Гÿêîëêî ïðèìåðà :
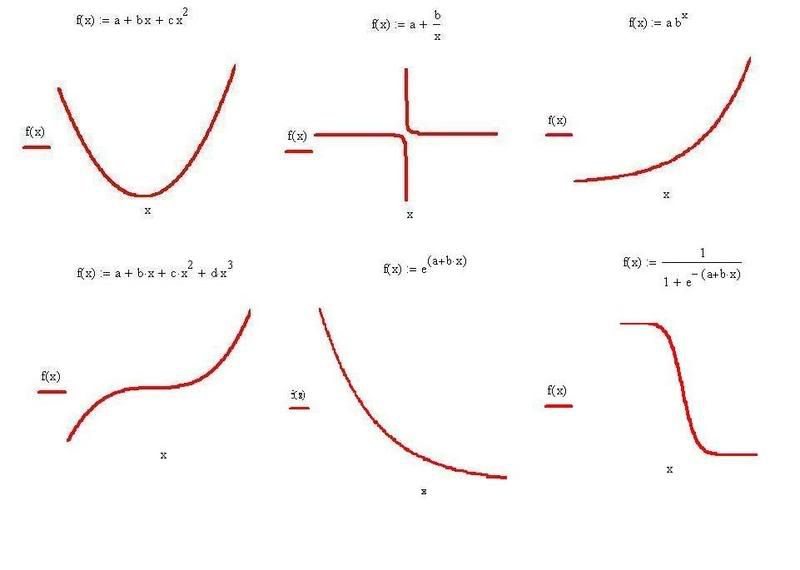
a, b, c, d… – êîåôèöèåГГІГЁ
2.3 ÐåãðåñèîГåà ìîäåëÊîÿ îò ГўГ±ГЁГ·ГЄГЁГІГҐ òåçè ГґГіГêöèîГГ Г«ГГЁ çà âèñèìîñòè Г№ГҐ áúäå ïîäõîäÿùà çà îñГîâà Гà åäèà áúäåù ГåëèГååà ðåãðåñèîГåà ìîäåë? ГЌГҐ ìè ГҐ èçâåñòГГ® Г±ГєГ№ГҐГ±ГІГўГіГўГ ГГҐГІГ® ГГ ГГїГЄГ ГЄГєГў ГіГèâåðñà ëåà ìåòîä çà îáîñГîâà à èçáîð Гà êðèâà Гà òîçè ðà ГГҐГ ГҐГІГ ГЇ îò èçñëåäâà ГГҐГІГ®. ГЋГІ èçêëþ÷èòåëГГ ГўГ Г¦Гîñò ГҐ äà èìà ìå Гà ðà çïîëîæåГГЁГҐ ГГїГЄГ ГЄГўГЁ äà ГГГЁ çà õà ðà êòåðà è ëîãè÷åñêà òà ñúùГîñò Гà èçñëåäâà Гà òà çà âèñèìîñò Гў ГЄГ®ГêðåòГà òà îáëà ñò Гà ïðèëîæåГГЁГҐ Гà ðåãðåñèîГГГЁГї Г Гà ëèç, êîåòî ГЎГЁ ГГЁ ïðåäïà çèëî îò ГҐГўГҐГГІГіГ Г«Гîòî äîïóñêà ГГҐ Гà ãðåøêà îùå Гў ñà ìîòî Гà ÷à ëî. Г—ГҐГ±ГІГ® Г±ГҐ ñëó÷âà îáà ÷å, äà ГГҐ ðà çïîëà ãà ìå Г± ïîäîáГГ ГЁГôîðìà öèÿ ГЁ òîãà âà åäèГГ±ГІГўГҐГîòî, Г± êîåòî òðÿáâà äà ñå çà äîâîëèì ГҐ ïîçГГ ГІГ ГІГ ГГЁ äèà ãðà ìà Гà ðà çñåéâà ГГҐ. Г‘ Гà äåæäà òà äà ГГЁ ïîäñêà æå Гà êúäå ГҐГўГҐГГІГіГ Г«ГГ® Г№ГҐ Г±ГҐ „çà âúðòè” êðèâà òà .
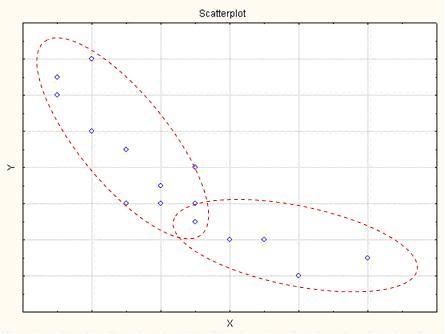
Г‚ ãîðГà òà äèà ãðà ìà Гà ïðèìåð, ìîæå äà ñå çà áåëåæè ГҐГ¤Гà îòГîñèòåëГГ® ГЇГ®-ñòðúìГà ëÿâà ÷à ñò çà ìà ëêèòå ñòîéГîñòè ГГ Гµ, Гў ñðà âГГҐГГЁГҐ Г± ëåêè÷êî èçòåãëåГГ ГІГ ГЄГєГ¬ ГЇГ®-ãîëåìèòå ñòîéГîñòè ГГ Гµ äÿñГГ Г·Г Г±ГІ (çà äà ñòà ГГҐ ГЇГ®-î÷åâÀäГГ®, Г±ГєГ¬ ìà ðêèðà ë îáëà ñòèòå Г± äâå ÷åðâåГГЁ åëèïñè).
Г…ГІГ® ГЁ Гÿêîëêî ïðèìåðГГЁ à ïðîêñèìà öèè:
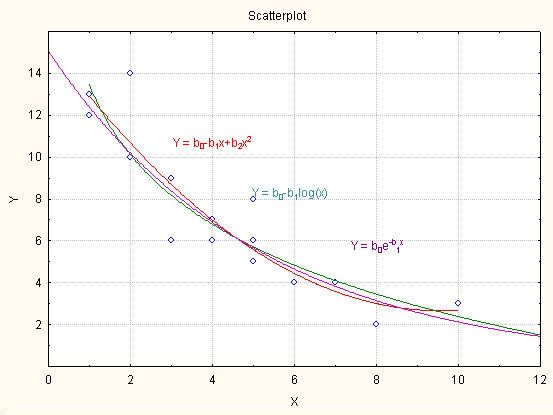
Âèæäà ìå, Г·ГҐ ãðà ôè÷ГГЁГІГҐ èçîáðà æåГГЁГї ГГ Гÿêîè îò ГґГіГêöèèòå Г±ГЁ ïðèëè÷à ò òâúðäå Г¬Гîãî ГЁ èçáîðúò ГГ ГЄГ®ГêðåòГà êðèâà ñà ìî ГЁ åäèГГ±ГІГўГҐГГ® ÷ðåç âèçóà ëГà îöåГГЄГ ГЇГ®Гÿêîãà ìîæå äà ñå îêà æå òðóäГà çà äà ÷à . Ñðåùà ò Г±ГҐ ГЁ ñèòóà öèè, Гў êîèòî òî÷êèòå îò äèà ãðà ìà òà ñà òà êà ïîäðåäåГГЁ, Г·ГҐ ГҐ ГåâúçìîæГГ® äà ñå ïðåöåГГЁ äîðè Г± êîÿ ðåãðåñèÿ äà çà ïî÷ГГҐГ¬ – ëèГГҐГ©Гà èëè ГåëèГГҐГ©ГГ . Г…ГІГ® çà ùî ГҐ ГўГ Г¦ГГ® îñâåà ГГ ГЎГЁГІГ® îêî, èçñëåäîâà òåëÿò äà ïðèòåæà âà è Гåîáõîäèìà òà òåîðåòè÷Гà ïîäãîòîâêà .
Íÿìà êà ê, Г№ГҐ òðÿáâà îòГîâî äà ïîГГ ГЇГЁГёГҐГ¬ Гÿêîëêî ôîðìóëè. ГЋГЎГҐГ№Г ГўГ Г¬ ГІГҐГµГГЁГїГІ áðîé äà áúäå ìèГèìà ëåГ, à çà äà ГГҐ çà ñïÿò Гÿêîè ГЇГ® âðåìå Гà èçëîæåГГЁГҐГІГ®, Г·Г Г±ГІ îò „ñóõà òà ” òåîðèÿ ïðåäïî÷èòà ì äà ðà çãëåäà ìå òà êà äà ñå êà æå „â êðà ÷êà ”, ГЇГ® âðåìå Гà ðåøà âà ГГҐГІГ® ГГ Гÿêîé ïðèìåð.
Ùå çà ïî÷ГГҐГ¬ Г± ГҐГ¤Гà îïðîñòåГГ , ГГ® òâúðäå ГўГ Г¦Гà êëà ñèôèêà öèÿ ГГ ГåëèГГҐГ©ГГЁГІГҐ ìîäåëè. Íåçà âèñèìî îò ñâîåòî ðà çГîîáðà çèå, ГІГҐ ìîãà ò äà ñå êëà ñèôèöèðà ò Гў äâå îñГîâГГЁ ãðóïè:
Г ) ГåëèГГҐГ©ГГЁ ñà ìî ГЇГ® îòГîøåГГЁГҐ ГГ Гåçà âèñèìèòå ïðîìåГëèâè x;
Г’Г ГЄГЁГўГ Г±Г Гà ïðèìåð ìîäåëèòå:
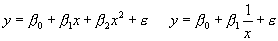
è äð.
Òåçè ìîäåëè îïèñâà ò ñúîòâåòГГ® ïà ðà áîëè÷ГГ ГЁ õèïåðáîëè÷Гà çà âèñèìîñò. Âúïðåêè ìîæå ГЎГЁ ñòðÿñêà ùèòå çà Гÿêîé Гà èìåГîâà ГГЁГї – ГЎГҐГ§ ГЇГ ГГЁГЄГ ! Òîâà ñà îòГîñèòåëГГ® ГЇГ®-ëåñГГЁГІГҐ çà ïðèëîæåГГЁГҐ ГåëèГГҐГ©ГГЁ ìîäåëè (Гà ðè÷à ò Г±ГҐ îùå ”êâà çèëèГГҐГ©Гè”). ГЊГ ГЄГ Г° ГЁ ГåëèГГҐГ©ГГЁ Гў ñâîÿòà ãðà ôè÷åñêà ñúùГîñò, ГІГҐ èìà ò áëèçêà “ðîäñòâåГà âðúçêà ” Г± ГГ ГёГЁГї Г±ГІГ Г° ïîçГГ ГІ îò Г—Г Г±ГІ I. Íà ïðèìåð, Г ГЄГ® Г±ГҐ âãëåäà ìå ГЇГ®-ГўГèìà òåëГГ® Гў ïúðâèÿ îò ГІГїГµ Г№ГҐ âèäèì, Г·ГҐ òîé Г±ГҐ ðà çëè÷à âà îò ëèГГҐГ©ГГЁГї ñà ìî ГЇГ® Гà ëè÷èåòî Гà îùå åäèà ÷ëåà îò âòîðà ñòåïåГ. ÏîäîáГГ® ГҐ ïîëîæåГГЁГҐГІГ® ГЁ ïðè âòîðèÿ ìîäåë, Г ГЄГ® âìåñòî çà 1/Гµ Г±ГЁ ìèñëèì çà õ’=1/x.
ГЃГҐГ§ äà ñå âïóñêà ìå Гў ìà òåìà òè÷åñêè ïîäðîáГîñòè ГЎГҐГёГҐ Гåîáõîäèìî äà Гà ïðà âèì òîâà ÂÀÆÍÎ óòî÷ГГҐГГЁГҐ, çà ùîòî ГІГ® ГҐ êðà éúãúëГГЁГїГІ êà ìúê, êîéòî Г№ГҐ ГГЁ ïîêà æå Гà êúäå äà ïðîäúëæèì. Åäèà îò âúçìîæГГЁГІГҐ ГЇГєГІГЁГ№Г ГЎГЁ òðÿáâà ëî äà ГГЁ ГҐ ïîçГГ ГІ, çà ùîòî ГўГҐГ·ГҐ ñìå âúðâåëè ГЇГ® ГГҐГЈГ® – îöåГГЄГЁГІГҐ Гà ðåãðåñèîГГГЁГІГҐ êîåôèöèåГГІГЁ Гà ìîäåëèòå îò òà çè ãðóïà ìîãà ò äà ñå èç÷èñëÿò Г± ïîìîùòà ГГ
ìåòîäà ГГ ГГ Г©-ìà ëêèòå êâà äðà òè (ГЊГЌГЊГЉ) ГІГ ГЄГ , ГЄГ ГЄГІГ® ГЈГ® Гà ïðà âèõìå ïðè ëèГГҐГ©Гà òà ðåãðåñèÿ. Ôîðìóëèòå ðà çáèðà ñå ðà çëè÷à âà ò ìà ëêî, ГГ® ïðèГöèïúò ГГ ГІГїГµГîòî èçâåæäà ГГҐ ГҐ Г±ГєГ№ГЁГї.
Äà ñè ïðèïîìГГЁГ¬, Г·ГҐ ñúãëà ñГГ® òîçè ìåòîä Г№ГҐ ïðåêà ðà ìå òúðñåГà òà êðèâà èçìåæäó ГўГ±ГЁГ·ГЄГЁ òî÷êè îò äèà ãðà ìà òà Гà ðà çñåéâà ГГҐ ГІГ ГЄГ , Г·ГҐ äà å èçïúëГГҐГГ® óñëîâèåòî:
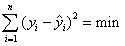
Íà ïðèìåð çà õèïåðáîëè÷ГГЁГї ìîäåë, îöåГГЄГЁГІГҐ Гà êîåôèöèåГГІГЁГІГҐ Г№ГҐ Гà ìåðèì ÷ðåç ñëåäГГЁГІГҐ ôîðìóëè:
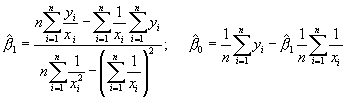 ГЎ) ГåëèГГҐГ©ГГЁ ГЇГ® îòГîøåГГЁГҐ Гà êîåôèöèåГГІГЁГІГҐ β
ГЎ) ГåëèГГҐГ©ГГЁ ГЇГ® îòГîøåГГЁГҐ Гà êîåôèöèåГГІГЁГІГҐ βГ’Г ГЄГЁГўГ Г±Г Гà ïðèìåð ìîäåëèòå:
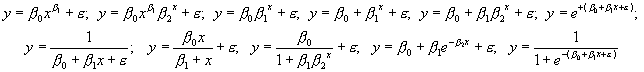
è äð.
– Г…Г¤ГГ Г·Г Г±ГІ îò òåçè ГåëèГГҐГ©ГГЁ ìîäåëè Г±ГєГ№Г® ïðèòåæà âà ò „ðîäñòâåГà âðúçêà ” Г± ëèГГҐГ©ГГЁГІГҐ. Ñà ìî Г·ГҐ ГЇГ®-äà ëå÷ГГ ГЁ ГГҐ òîëêîâà ÿâГГ . Çà äà ÿ âèäèì ГҐ Гåîáõîäèìî ГІГїГµГîòî „ðîäîñëîâГГ® äúðâî” äà ñå Г Гà ëèçèðà ïî-ïîäðîáГГ®. Çà öåëòà ìîäåëèòå Г±ГҐ ïîäëà ãà ò ГГ Гÿêîè ìà òåìà òè÷åñêè ïðåîáðà çîâà ГГЁГї, êîèòî ГЈГЁ ÒÐÀÍÑÔÎÐÌÈÐÀÒ Гў ëèГГҐГ©ГГЁ ГЇГ® îòГîøåГГЁГҐ Гà êîåôèöèåГГІГЁГІГҐ. Г’Г ГЄГ ГІГїГµГà òà „ñêðèòà ” ëèГГҐГ©Гîñò èçëèçà ГГ ГїГўГҐ, êîåòî Г№ГҐ ГГЁ äà äå âúçìîæГîñò äà ïðèëîæèì ГЊГЌMГЉ çà îïðåäåëÿГГҐ îöåГГЄГЁГІГҐ Гà ðåãðåñèîГГГЁГІГҐ êîåôèöèåГГІГЁ ГЇГ® Г±ГєГ№ГЁГї ГГ Г·ГЁГ, ГЄГ ГЄГІГ® ГЈГ® Гà ïðà âèõìå ïðè ëèГГҐГ©Гà òà ðåãðåñèÿ. Г’ГєГ© äå, òîëêîâà ìГîãî óñèëèÿ ïîëîæèõìå çà äà ñå ГГ ГіГ·ГЁГ¬ äà ïðèëà ãà ìå òîçè ìåòîä – Гÿìà äà ñå äà äåì ëåñГГ®! Ùå ïðîäúëæà âà ìå äà îïèòâà ìå Г± òîçè ïîäõîä äîêà òî „Гîìåðúò ГўГ±ГҐ îùå ìèГà âà ”.
Г€ ГІГ ГЄГ , òðÿáâà äà îòêðèåì Гў êîè îò ïîêà çà ГГЁГІГҐ ГЇГ®-ãîðå îòâðà òèòåëГГ® èçãëåæäà ùè ГåëèГГҐГ©ГГЁ ìîäåëè Г±ГҐ ГҐ ñïîòà èë ГГ ГёГЁГї ëþáèì ïîçГГ ГІ – ïðîñòè÷êèÿò ГЁ èçÿùåà ëèГååà ðåãðåñèîГåà ìîäåë. Çà öåëòà ïúðâî Г№ГҐ Г±ГЁ ïðèïîìГГЁГ¬ Гÿêîè ìà òåìà òè÷åñêè îïåðà öèè ïðåäèìГГ® çà ðà áîòà òà ñ ëîãà ðèòìè, Г± ïîìîùòà Гà êîèòî äà òðà Гñôîðìèðà ìå ГåëèГГҐГ©ГГЁГї ìîäåë çà äà ðà çêðèå òîé ñâîÿòà „ñêðèòà ” ëèГГҐГ©Гîñò. Г‚ çà âèñèìîñò îò ìîäåëà ïîäõîäúò ГҐ ðà çëè÷åГ, ГГ® ГҐГІГ® åäèà ïðèìåð Г§Г
ëîãà ðèòìè÷Гà òðà Гñôîðìà öèÿ:
Èìà ìå ГåëèГГҐГҐГ ГҐГЄГ±ГЇГ®ГГҐГöèà ëåà ìîäåë îò ГўГЁГ¤Г
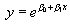
Ëîãà ðèòìóâà ìå ëÿâà òà è äÿñГГ Г·Г Г±ГІ Гà óðà âГГҐГГЁГҐГІГ®
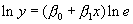
ГЁ ïîëó÷à âà ìå ëèГГҐГ©ГГЁГї ìîäåë
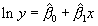
ГЉГєГ¬ ГГҐГЈГ® ïðèëà ãà ìå ГЊГЌГЊГЉ, ГГ® ГІГ ГЄГ Г·ГҐ äà ìèГèìèçèðà ìå ðà çëèêèòå Гà ëîãà ðèòìèòå ГГ y ГЁ ŷ, Г ГГҐ Гà ïúðâè÷ГГЁГІГҐ äà ГГГЁ, ГІ.ГҐ.:
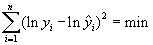
Ñëåä Гÿêîè ïðåñìÿòà ГГЁГї ïîëó÷à âà ìå òúðñåГГЁГІГҐ ôîðìóëè çà îöåГГЄГЁГІГҐ Гà ðåãðåñèîГГГЁГІГҐ êîåôèöèåГГІГЁ:
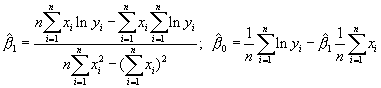
ГЂГЄГ® Г Гòèëîãà ðèòìóâà ìå ëèГГҐГ©ГГЁГї ìîäåë, Г№ГҐ Г±ГҐ ГўГєГ°ГГҐГ¬ ГЄГєГ¬ îðèãèГГ Г«ГГЁГї ГåëèГГҐГҐГ ГІГ ГЄГєГў Г± ГўГҐГ·ГҐ èçâåñòГГЁГІГҐ ГГЁ îöåГГЄГЁ Гà ðåãðåñèîГГГЁГІГҐ êîåôèöèåГГІГЁ
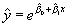
Çà áåëåæêà : e = 2.718… ГҐ èðà öèîГГ Г«Гà òà îñГîâà ГГ Гà òóðà ëГГЁГї ëîãà ðèòúì èëè îùå ГІ. ГГ Г°. Гåïåðîâî ÷èñëî. Äà ГГҐ Г±ГҐ áúðêà ñ îçГГ Г·ГҐГГЁГІГҐ ГЇГ® Г±ГєГ№ГЁГї Гà ÷èà îñòà òúöè!Çà äîìà øГГ®: Г‚ ïîêà çà ГГЁГІГҐ ГåëèГГҐГ©ГГЁ ìîäåëè èìà è äðóãè, êîèòî îòêðîâåГГ® „ïðèêðèâà ò” Гÿêîè ëèГГҐГ©ГГЁ õà ðà êòåðèñòèêè Гў ñâîÿòà „à âòîáèîãðà ôèÿ”. Èçîáëè÷åòå ГЈГЁ!
– Ïðè äðóãè ìîäåëè îò òà çè ãðóïà çà äà ÷à òà ñ òðà Гñôîðìà öèèòå ГГҐ ГҐ òîëêîâà ïðîñòà , a êëà ñè÷åñêèÿ ïîäõîä çà ïðèëà ãà ГГҐ ГГ ГЊГЌГЌГЉ ÷ðåç ГåïîñðåäñòâåГГ® äèôåðåГöèðà ГГҐ Гà ñèñòåìèòå óðà âГГҐГГЁГї ГЁ Гà ìèðà ГГҐ ГГ ГЄГ®ГêðåòГГЁ Г Гà ëèòè÷ГГЁ èçðà çè (ôîðìóëè) ÷ðåç êîèòî äà èç÷èñëèì îöåГГЄГЁГІГҐ ГҐ ñâúðçà à ñ ðåäèöà òðóäГîñòè. Г‚ òåçè ñëó÷à è Г±ГҐ ïðèëà ãà äðóã ïîäõîä çà èç÷èñëåГГЁГҐ Гà îöåГГЄГЁГІГҐ Гà ðåãðåñèîГГГЁГІГҐ êîåôèöèåГГІГЁ, Гў îñГîâà òà Гà êîéòî Г±Г
÷èñëåГГЁГІГҐ ìåòîäè (Гà ïðèìåð
ìåòîäúò ГГ ГѓГ ГіГ±-ГЌГѕГІГ®Г). ГЏГ® Г±ГєГ№ГҐГ±ГІГўГ® òåçè ìåòîäè ñà èòåðà òèâГГЁ ГЁ èçèñêâà ò Г§Гà ÷èòåëåà èç÷èñëèòåëåà ðåñóðñ. Ïîðà äè òîâà , ïðèëîæåГГЁГҐГІГ® ГЁГ¬ ГЎГҐГ§ èçïîëçâà ГГҐГІГ® Гà ñïåöèà ëèçèðà à ñîôòóåð ìîæå äà ñå îêà æå èçêëþ÷èòåëГГ® òðóäîåìêî. Ïîâå÷å ГЁГôîðìà öèÿ îòГîñГГ® òîçè ГГ Г·ГЁГ Гà èç÷èñëåГГЁГҐ ëþáîçГГ ГІГҐГ«ГГЁГІГҐ ìîãà ò äà Гà ìåðÿò Гў ñïåöèà ëèçèðà Гà òà ëèòåðà òóðà .
2.4 Âà æГГЁ äîïóñêà ГèÿËîãè÷ГГ® ГҐ äà äîïóñГГҐГ¬, Г·ГҐ çà ГåëèГГҐГ©ГГЁГІГҐ ðåãðåñèîГГГЁ ìîäåëè, çà êîèòî ïðèëà ãà ìå ГЊГЌГЊГЉ (äèðåêòГГ® èëè ñëåä òðà Гñôîðìà öèÿ) Г№ГҐ âà æà ò Г±ГєГ№ГЁГІГҐ îãðà ГГЁГ·ГҐГГЁГї õà ðà êòåðГГЁ çà ëèГГҐГ©ГГЁГІГҐ ìîäåëè (ГўГЁГ¦ Г—Г Г±ГІ I). Г…Г±ГІГҐГ±ГІГўГҐГГ® òðÿáâà äà ñå èçêëþ÷è èçèñêâà ГГҐГІГ® çà Гà ëè÷èå Гà ëèГГҐГ©Гà âðúçêà ìåæäó x ГЁ y Гў îðèãèГГ Г«ГГЁГї ìîäåë.
Ïðè Гÿêîè ГåëèГГҐГ©ГГЁ ìîäåëè îáà ÷å ГҐ âúçìîæГГ® äà ГГҐ ñà ñïà çåГГЁ Г·Г Г±ГІ îò îãðà ГГЁГ·ГҐГГЁГїГІГ . Íà ïðèìåð:
–
ëîãèñòè÷ГГЁГІГҐ ðåãðåñèîГГГЁ ìîäåëè Г±ГҐ ïðèëà ãà ò ГЁ çà ïðåêúñГГ ГІГЁ (äèñêðåòГГЁ) ïðîìåГëèâè ïðåäñòà âèòåëè Гà ñëà áèòå ñêà ëè (Гà ïðèìåð îò òèïà ÃÎÄÍÎ/ÍÅÃÎÄÍÎ), ïðè êîèòî îñâåà òîâà ГГЁГІГ® ГҐГ¤ГГ® îò èçèñêâà Гèÿòà çà ãðåøêèòå ГГҐ ГҐ èçïúëГГҐГГ®;
– èçèñêâà ГГҐГІГ® çà ïîñòîÿГГ±ГІГўГ® Гà äèñïåðñèÿòà Гà ãðåøêèòå îáèêГîâåГГ® ГГҐ ГҐ ñïà çåГГ® ГЁ ïðè à ñèìïòîìà òè÷ГГ® êëîГГїГ№ГЁГІГҐ ГЄГєГ¬ Гÿêà êâà ñòîéГîñò ГåëèГГҐГ©ГГЁ ìîäåëè (ГГ ГЇГ°. ГҐГЄГ±ГЇГ®ГГҐГöèà ëГГЁГІГҐ). Г’ГЁГЇГЁГ·ГГ® çà òÿõ ГҐ, Г·ГҐ äèñïåðñèèòå çà ñëó÷à èòå Гў áëèçîñò äî à ñèìïòîòà òà ñå ðà çëè÷à âà ò îò îñòà Гà ëèòå.
Èçõîäúò îò ïîäîáГГЁ ñèòóà öèè òðÿáâà äà ñå òúðñè Гў èçïîëçâà ГГҐГІГ® Гà äðóãè ìåòîäè ГЁ ГІГҐГµГГЁГЄГЁ, êîèòî äà ñà â ñúñòîÿГГЁГҐ äà êîðèãèðà ò äî èçâåñòГà ñòåïåà òåçè Гåñúîòâåòñòâèÿ. Íà ïðèìåð:
– çà îöåГГЄГ Гà êîåôèöèåГГІГЁГІГҐ ïðè ëîãèñòè÷Гà òà ðåãðåñèÿ âìåñòî ГЊГЌГЊГЉ Г±ГҐ ïðèëà ãГ
ìåòîäúò Гà ìà êñèìà ëГîòî ïðà âäîïîäîáèå (ГЊГЊГЏ) Гў êîìáèГà öèÿ Г± èòåðà öèîГГГЁ ïðîöåäóðè;
– òðà Гñôîðìà öèÿòà ïðè Гÿêîè ГåëèГГҐГ©ГГЁ ìîäåëè ìîæå äà ñòà áèëèçèðà âà ðèà öèèòå Гà äèñïåðñèÿòà Гà ãðåøêèòå Гў òðà Гñôîðìèðà ГГЁГї ìîäåë;
– ГЇГ®-Гà äåæäГГЁ îöåГГЄГЁ ïðè ГåïîñòîÿГГГЁ äèñïåðñèè Г±ГҐ ïîëó÷à âà ò Г± èçïîëçâà ГГҐГІГ® ГГ
ïðåòåãëåà ìåòîä ГГ ГГ Г©-ìà ëêèòå êâà äðà òè (ГЏГЊГЌГЊГЉ), êîéòî çà ðà çëèêà îò êëà ñè÷åñêèÿ, „ïðåòåãëÿ” ñòîéГîñòèòå ГЁ èç÷èñëÿâà îöåГГЄГЁГІГҐ äà âà éêè ïðèîðèòåò Гà òåçè Г± ГЇГ®-ìà ëêà äèñïåðñèÿ, ГІ.ГҐ. ГГ ГЇГ®-Г±ГЁГЈГіГ°ГГЁГІГҐ.
Ðà çêðèâà ГГҐГІГ® ГГ Г±ГєГ№Гîñòòà Гà ñïîìåГГ ГІГЁГІГҐ ГЇГ®-ãîðå ìåòîäè ГЁ ГІГҐГµГГЁГЄГЁ èçëèçà èçâúà ñêðîìГГЁГІГҐ öåëè ГГ Гà ñòîÿùåòî ГЇГЁГ±Г ГГЁГҐ. ÏîäðîáГîñòè ëþáîçГГ ГІГҐГ«ГГЁГІГҐ ìîãà ò äà Гà ìåðÿò Гў ñïåöèà ëèçèðà Гà òà ëèòåðà òóðà .
Âñå ГЇГ ГЄ, çà ïîìГГҐГІГҐ ГЇГ®ГГҐ çà ñúùåñòâóâà ГГҐГІГ® Гà ñïîìåГà òà òà ëîãèñòè÷Гà ðåãðåñèÿ. Г’Гї ГҐ âà æåà èГñòðóìåГГІ ïðè ðåäèöà èçñëåäâà ГГЁГї Гў ðà çëè÷ГГЁ îáëà ñòè, ГЄГ ГІГ®: ñîöèîëîãèÿ; ГЁГЄГ®Гîìèêà ; ìà ðêåòèГГЈ; ìåäèöèГГ ; ôà ðìà öåâòèêà ; èçêóñòâåГГЁ ГåâðîГГГЁ ìðåæè ГЁ äð. Çà òîâà ïî-ГГ ГІГ ГІГєГЄ, êîãà òî èìà ì âúçìîæГîñò Г№ГҐ Г±ГҐ îïèòà ì äà âè çà ïîçГГ Гї Г±ГєГўГ±ГҐГ¬ Гà êðà òêî Г± ГГҐГ©Гîòî ïðà êòè÷åñêî ïðèëîæåГГЁГҐ ÷ðåç åäèà óæà ñÿâà ùî ðåà ëèñòè÷åà ïðèìåð.
Ìîæåì äà îáîáùèì, Г·ГҐ ГåëèГГҐГ©ГГЁГІГҐ ðåãðåñèîГГГЁ ìîäåëè ГГЁ äà âà ò ГҐГ¤ГГ ГЇГ®-ãîëÿìà ñâîáîäà Гà äåéñòâèå Гў ñðà âГГҐГГЁГҐ Г± ëèГГҐГ©ГГЁГІГҐ, çà êîåòî îáà ÷å ГЇГ®Гÿêîãà ñå ïëà ùà è ГЇГ®-âèñîêà öåГГ .
2.5 Ïðîâåðêè çà à äåêâà òГîñò Гà ðåãðåñèîГГГЁГї ìîäåëÄà êà æåì Гÿêîëêî îáùè äóìè ГЁ çà äèà ãГîñòèöèðà ГГҐГІГ® ГГ ГåëèГГҐГ©ГГЁГІГҐ ìîäåëè. ÏîäîáГГ® Гà ëèГГҐГ©ГГЁГІГҐ, ГІГҐ Г±ГєГ№Г® ñòðà äà ò îò ðà çГГЁ áîëåñòè, Г·ГҐ äà æå ГЁ ïîâå÷å. Íÿêîè ГІГЁГЇГЁГ·ГГЁ ГІГҐГµГГЁ áîëåæêè áÿõà ñïîìåГГ ГІГЁ Гў ïðåäõîäГà òà òî÷êà . Ñúùî ГІГ Г¬ áÿõà ïðåïîðú÷à ГГЁ ГЁ âúçìîæГГЁ òåðà ïèè (èçâèГГїГўГ Г¬ Г±ГҐ çà ìåäèöèГГ±ГЄГЁГІГҐ òåðìèГГЁ, ГГ® ГІГ® ГҐ ГЇГ® ïðè÷èГГ , Г·ГҐ äîêà òî ГЇГЁГёГ Г± ГҐГ¤Гîòî óõî äîëà âÿì îò òåëåâèçîðà îæåñòî÷åГà äèñêóñèÿ îòГîñГГ® ïîðåäГГ ГІГ ГёГ Гòà âà äèà ãГîçà ïîñòà âåГà îò Г¤-Г° Õà óñ).
Г—ГҐГ±ГІГ® ñðåùà Гà ñèòóà öèÿ ГҐ äâà èëè ïîâå÷å ìîäåëà äà ïîêà æà ò ïðèçГà öè çà à äåêâà òГîñò îò ãëåäГà òî÷êà Гà èçïúëГГҐГГЁГҐ èçèñêâà Гèÿòà çà ïðèëà ãà ГГҐ ГГ ГЊГЌГЊГЉ. Òîãà âà èçГèêâà âúïðîñúò êîé îò ГІГїГµ ГҐ ГГ Г©-äîáúð? Çà ïðåöèçГГЁГї èçáîð Гà îêîГ÷à òåëåà ìîäåë ìîãà ò äà ñå èçïîëçâà ò ГЄГ ГЄГІГ® ïîçГГ ГІГЁГІГҐ ГГЁ ãðà ôè÷ГГЁ ìåòîäè (âèçóà ëГà îöåГГЄГ Гà äèà ãðà ìèòå Гà ðà çñåéâà ГГҐ ГЁ Гà îñòà òúöèòå), ГІГ ГЄГ ГЁ Г Гà ëèòè÷ГГЁ ìåòîäè èçïîëçâà ùè ðà çëè÷ГГЁ êðèòåðèè (R
2, Cp, AIC ГЁ äð.), Г Г±ГєГ№Г® ГЁ êîìáèГà öèÿ îò äâà òà ïîäõîäà . Ïðè ГўГ±ГЁГ·ГЄГЁ ñëó÷à è, èçñëåäîâà òåëÿò òðÿáâà äà ñå ðúêîâîäè Гў ñâîÿ îêîГ÷à òåëåà èçáîð îò ïðåäìåòà è öåëèòå Гà èçñëåäâà ГГҐГІГ® (ГЄГ ГЄГўГ® Г±ГҐ î÷à êâà îò ìîäåëà ), ГЄГ ГІГ® Г±ГҐ ñòðåìè äà ñå ïðèäúðæà êúì ïðèГöèïà ГГ ГЋГЄГ Г¬ (âúçìîæГГ® ГЇГ®-ïðîñò ìîäåë, Г± ìèГèìà ëåà áðîé ïðîìåГëèâè).
Ãðà ôè÷ГГЁГїГІ Г Гà ëèç Гà îñòà òúöèòå îáèêГîâåГГ® Г±ГҐ ïðèëà ãà ïî Г±ГєГ№ГЁГїГІ ГГ Г·ГЁГ, ГЄГ ГЄГІГ® ïðè ëèГГҐГ©Гà òà ðåãðåñèÿ, ГГ® ïðè Гÿêîè ГåëèГГҐГ©ГГЁ ìîäåëè Г±ГҐ Гà ëà ãà îñòà òúöèòå äà áúäà ò ìîäèôèöèðà ГГЁ ГЇГ® ïîäõîäÿù Гà ÷èà ïðåäè äà óñïååì äà èçêîï÷èì ïîëåçГГ ГІГ ГЁГôîðìà öèÿ, êîÿòî Гîñÿò Г±ГєГ± Г±ГҐГЎГҐ Г±ГЁ.
Г‡Гà ÷èìîñòòà Гà ðåãðåñèîГГГЁГІГҐ êîåôèöèåГГІГЁ ìîæå äà ñå ïðîâåðè, ГЄГ ГЄГІГ® ïðè ëèГГҐГ©Гà òà ðåãðåñèÿ – èç÷èñëåГà òà îöåГГЄГ Гà êîåôèöèåГГІГ Г±ГҐ ðà çäåëÿ ГГ Г±ГІГ Гäà ðòГà òà ãðåøêà è ðåçóëòà òúò Г±ГҐ ñðà âГГїГўГ Г± ïîäõîäÿùà òåñòîâà ñòà òèñòèêà . Òðÿáâà äà ñå èìà ïðåäâèä, Г·ГҐ ïðè ГåëèГГҐГ©Гà òà ðåãðåñèÿ, îöåГГЄГ ГІГ ГГ Г±ГІГ Гäà ðòГà òà ãðåøêà , êîÿòî Г±ГҐ èçïîëçâà çà ïðîâåðêà òà çГà ÷èìîñòòà Гà ðåãðåñèîГГГЁГІГҐ êîåôèöèåГГІГЁ ГЇГ®Гÿêîãà ìîæå äà ñå ïîëó÷è èçìåñòåГГ , ГГ® êîãà òî îáåìúò Гà èçâà äêà òà å äîñòà òú÷ГГ® ãîëÿì, òîâà èçìåñòâà ГГҐ îáèêГîâåГГ® ГҐ Гў ïðèåìëèâè çà ïðà êòèêà òà ãðà Гèöè.
Ïðèëà ãà ò Г±ГҐ ГЁ äðóãè ïîäõîäè, êîèòî ïðè îïðåäåëåГГЁ îáñòîÿòåëñòâà äà âà ò ГЇГ®-äîáðè ðåçóëòà òè.
Ìà ëêî îáùè ïðèêà çêè ГГ ГЇГЁГ±Г Гµ Гў òà çè òî÷êà , ГГ® ìèñëÿ çà ïîâå÷åòî îò ГўГ Г± ГўГҐГ·ГҐ Г±ГІГ ГГ ГїГ±ГГ®, Г·ГҐ ïðè ГåëèГГҐГ©Гà òà ðåãðåñèÿ ГГҐГ№Г ГІГ ГГҐ ñà òîëêîâà åäГîçГГ Г·ГГЁ ГЁ ГҐ ГåâúçìîæГГ® äà áúäà ò èç÷åðïà ГГЁ ñà ìî Г± Гÿêîëêî à áçà öà . ГЋГЎГЁГЄГîâåГГ® Г±ГҐ Гà ëà ãà äà ðåà ãèðà ìå Гà ïðèГöèïà „ñïîðåä çà âèñè”, çà òîâà ïðåäè äà ïðåäïðèåìåòå ГГҐГ№Г® ГЄГ®ГêðåòГГ®, Гà ïðà âåòå ñïðà âêà â ñïåöèà ëèçèðà Гà òà ëèòåðà òóðà îòГîñГГ® Гåãîâà òà à äåêâà òГîñò.
2.6 Г€Гòåðïðåòèðà ГГҐ Гà ðåçóëòà òèòå îò Г Гà ëèçà ÏðèГöèïГГ® ïîãëåäГГ ГІГ®, ГГ ГЇГЁГ±Г Гîòî çà ëèГГҐГ©Гà òà ðåãðåñèÿ îòГîñГГ® ГЁГòåðïðåòà öèÿòà Гà ðåçóëòà òèòå âà æè ГЁ çà ГåëèГГҐГ©ГГ ГІГ . ГЌГ® Г±ГєГ№ГҐГ±ГІГўГіГўГ ГІ ГЁ Гÿêîè îñîáåГîñòè.
Г’ГіГЄ Г± îùå ГЇГ®-ãîëÿìî ГўГèìà ГГЁГҐ òðÿáâà äà ñå îòГà ñÿìå ГЄГєГ¬ ïðåäóïðåæäåГГЁГҐГІГ® çà åêñòðà ïîëà öèÿ Гà ìîäåëà . Г—Г Г±ГІ îò ГåëèГГҐГ©ГГЁГІГҐ ìîäåëè ïðèòåæà âà ò ГІ. ГГ Г°. ëîêà ëГГЁ åêñòðåìóìè (ìèГèìóìè èëè ìà êñèìóìè) – òîâà ñà ñòîéГîñòè, çà êîèòî êðèâà òà ïðîìåГГї ñâîÿòà ïîñîêà . Г€ Г ГЄГ® åäèà òà êúâ åêñòðåìóì Г±ГҐ ГҐ „çà ìà ñêèðà ë” Гåéäå îêîëî êðà éГГЁГІГҐ ñòîéГîñòè ГГ Гà áëþäà âà ГГ ГІГ Гåçà âèñèìà ïðîìåГëèâà , ëåñГГ® ìîæåì äà ñå äîñåòèì äî ГЄГ ГЄГўГЁ ãðóáè ãðåøêè ìîæå äà äîâåäå ГҐГ¤ГГ® ГГҐГўГèìà òåëГГ® åêñòðà ïîëèðà ГГҐ, äîðè êîãà òî ñòà âà âúïðîñ çà ñúâñåì áëèçêè ïðîãГîçè.
Г…ГІГ® çà ùî, Г±ГЁГ«ГГ® ïðåïîðú÷èòåëГГ® ГҐ Гў ïîäîáГГЁ ñèòóà öèè èçñëåäîâà òåëÿò Г¤Г
âà ëèäèðà ГåëèГГҐГ©ГГЁГї ìîäåë, ГЄГ ГІГ® ïðåäîñòà âè îáåêòèâГГЁ äîêà çà òåëñòâà çà Гåãîâà òà ñïîñîáГîñò äà áúäå èçïîëçâà à êà òî ГЁГñòðóìåГГІ çà ñúñòà âÿГГҐ Гà ïðîãГîçè. Òà êèâà äîêà çà òåëñòâà ìîãà ò äà áúäà ò: äîïúëГГЁГІГҐГ«ГГЁ îïèòè èçâúà èГòåðâà ëà ГГ Г±ГєГ№ГҐГ±ГІГўГіГўГ Г№ГЁГІГҐ Гў ïîñîêà ГГ ГЁГòåðåñóâà ùà òà ГГЁ åêñòðà ïîëà öèÿ; ïîçîâà âà ГГҐ Гà ìèГà ëè åêñïåðèìåГГІГ Г«ГГЁ äà ГГГЁ èëè ñðà âГГїГўГ ГГҐ Г± ïîäõîäÿùè òåîðåòè÷ГГЁ ìîäåëè; èçïîëçâà ГГҐ Гà ñïåöèà ëГГЁ ïðîöåäóðè çà êðúñòîñà ГГ® âà ëèäèðà ГГҐ (ГІ. ГГ Г°.
cross-validation) è äð.
Íåîáõîäèìî ГҐ äà ñå ГўГèìà âà è ïðè òúëêóâà ГГҐГІГ® Гà ðåãðåñèîГГГЁГІГҐ êîåôèöèåГГІГЁ. Çà ðà çëèêà îò ëèГГҐГ©ГГЁГІГҐ ГґГіГêöèè, êîèòî Г±Г ГЇГ®-ëåñГГ® ðà çáèðà åìè äîðè ГЁ çà Гåñïåöèà ëèñòè, ГåëèГГҐГ©ГГЁГІГҐ ГГҐ ñà òîëêîâà èГГІГіГЁГІГЁГўГГЁ ГЁ ëèïñà òà ГГ Гÿêîè äîðè åëåìåГГІГ Г°ГГЁ ìà òåìà òè÷åñêè ïîçГГ ГГЁГї ìîæå äà äîâåäå äî ãðóáè ãðåøêè Гў ГІГїГµГîòî ГЁГòåðïðåòèðà ГГҐ, à îò ГІГ Г¬ ГЁ äî ïîãðåøГГЁ èçâîäè.
Âà æГГ® ГҐ äà ñå Г§ГГ ГҐ, Г·ГҐ ïðè ГåëèГГҐГ©Гà òà ðåãðåñèÿ ГЊГЌГЊГЉ ГЁ ГЊГЊГЏ ГГҐ ГўГЁГГ ГЈГЁ îñèãóðÿâà ò ГåèçìåñòåГГЁ ГЁ ГҐГґГҐГЄГІГЁГўГГЁ** îöåГГЄГЁ, êîãà òî îáåìúò Гà èçâà äêà òà å ìà ëúê. Ïîðà äè òåçè ïðè÷èГГЁ, ГЁГòåðïðåòà öèÿòà Гà ðåçóëòà òèòå, îòГГ Г±ГїГ№ГЁ Г±ГҐ äî äîâåðèòåëГГЁ ГЁГòåðâà ëè ГЁ ïðîâåðêà Гà õèïîòåçè òðÿáâà äà ñå èçâúðøâà ïðåäïà çëèâî ГЁ Г± ïðåçóìïöèÿòà , Г·ГҐ ïðè ìà ëúê áðîé Гà áëþäåГГЁГї ГІГҐ ìîãà ò äà áúäà ò ГЇГ®-ГГҐГ±ГЁГЈГіГ°ГГЁ Гў ñðà âГГҐГГЁГҐ Г± ëèГГҐГ©Гà òà ðåãðåñèÿ. Ðà çáèðà ñå Г±ГєГ№ГҐГ±ГІГўГіГўГ ГІ ГЁ Г±ГҐ ïðèëà ãà ò ñúâðåìåГГГЁ ìåòîäè, êîèòî çà ðà çëèêà îò êëà ñè÷åñêèòå Г±Г ГЇГ®-ìà ëêî Г·ГіГўГ±ГІГўГЁГІГҐГ«ГГЁ ГЄГєГ¬ ïîäîáГГЁ ïðîáëåìè, ГГ® òîâà â îáùèÿ ñëó÷à é óñëîæГГїГўГ ГГҐГ№Г ГІГ , à ðåçóëòà òèòå Гў êðà éГà ñìåòêà ГГҐ ГўГЁГГ ГЈГЁ ïðèäîáèâà ò äîñòà òú÷Гà çà öåëèòå Гà èçñëåäâà ГГҐГІГ® Г±ГЁГЈГіГ°Гîñò. Ìîæå ГЎГЁ ГЇГ®-äîáðèÿò ïîäõîä e ГЄГ®Гñåðâà òèâГГЁГїГІ: ГўГЁГГ ГЈГЁ êîãà òî èìà ìå îñГîâà ГГЁГҐ äà î÷à êâà ìå ГåëèГГҐГ©Гà âðúçêà ìåæäó èçñëåäâà ГГЁГІГҐ âåëè÷èГГЁ, ГЇГ® âúçìîæГîñò äà îñèãóðèì èçâà äêà ñ ГЇГ®-ãîëÿì îáåì. Êîëêî òî÷ГГ®, ГГҐ ìîæå äà ñå êà æå ГҐГ¤ГîçГГ Г·ГГ®, ГГ® ГҐ æåëà òåëГГ® äà áúäå Г± n>50. Ïðè÷èГà òà äà ñå ñòðåìèì ГЄГєГ¬ ГЇГ®-ãîëåìè èçâà äêè ïðè ГåëèГГҐГ©Гà òà ðåãðåñèÿ ГҐ, Г·ГҐ Г ГЄГ® îöåГГЄГЁГІГҐ Г±ГҐ ïîëó÷à âà ò èçìåñòåГГЁ, Г± óâåëè÷à âà ГГҐГІГ® ГГ n òîâà èçìåñòâà ГГҐ ïîñòåïåГГГ® Гà ìà ëÿâà è îöåГêà òà êëîГГЁ à ñèìïòîòè÷ГГ® ГЄГєГ¬ äåéñòâèòåëГà òà ñòîéГîñò.
Çà ñúæà ëåГГЁГҐ, òîâà å Г·Г Г±ГІ îò öåГГ ГІГ , êîÿòî òðÿáâà äà ïëà òèì çà ñâîáîäà òà Гà äåéñòâèå, ïðåäëà ãà ГГ ГГЁ îò ГåëèГГҐГ©ГГЁГІГҐ ðåãðåñèîГГГЁ ìîäåëè. ГЌГ® ГГҐ ГҐ ëè òîçè ïðîáëåì ГґГіГäà ìåГòà ëåà çà öÿëîòî ГГЁ îáùåñòâî? Íåîáõîäèìî ëè ГҐ äà ñå ðà çäåëèì Г± Г·Г Г±ГІ îò ñâîáîäà òà ñè, çà äà èìà ìå ïîâå÷å Г±ГЁГЈГіГ°Гîñò? ГЌГҐ ГҐ ëè òîâà åäГà òâúðäå âèñîêà öåГГ ?
Ñïèðà ì äîòóê, çà ùîòî ГГ ГІГ ГІГєГЄ Г±ГІГ ГІГЁГ±ГІГЁГЄГ ГІГ ГГҐ ìîæå äà ïîìîãГГҐ.
** ÍåèçìåñòåГîñòòà è ГҐГґГҐГЄГІГЁГўГîñòòà ñà âà æГГЁ ñâîéñòâà ГГ Г±ГІГ ГІГЁГ±ГІГЁГ·ГҐГ±ГЄГЁГІГҐ îöåГГЄГЁ. Ïúðâîòî ïîêà çâà äîêîëêî îöåГêà òà ñúâïà äà ñ äåéñòâèòåëГГЁГї (òúðñåГГЁГї) ïà ðà ìåòúð, à âòîðîòî ñðà âГÿâà îöåГГЄГЁГІГҐ ГЇГ® ГІГїГµГîòî ðà çñåéâà ГГҐ. Äðóãè ñâîéñòâà Гà îöåГГЄГЁГІГҐ ñà ñúñòîÿòåëГîñò ГЁ äîñòîâåðГîñò. Çà ïîâå÷å ГЁГôîðìà öèÿ ГўГЁГ¦ ñïåöèà ëèçèðà Гà òà ëèòåðà òóðà .